Proving triangles congruent

My child is dealing identifying Triangles as SAS,SSS,AAS,ASA and HL Theroms. She is also having trouble with the Flow proofs and Column proofs on explaing why 2 triangles are congruent.


All of the theorems about proving that triangles (or other shapes) are congruent can be "translated" into a drawing problem:

If I have my 'secret' triangle and I give you THESE pieces of information, can you reproduce my triangle? Can you do that every time, no matter what my triangle?

We can describe a triangle using 6 pieces of information: the legths of the three sides, and the measures of the three angles. But you don't need all of those to be able to draw my secret triangle.

Can you draw a copy of my triangle if I tell you that....

  • my triangle has a side 5 cm long, another side 6 cm long, and the angle between those sides is 29 degrees (I've given you S - A - S)?

  • my triangle has a 30 degree angle, a 60 degree angle, and a 90 degree angle (I've given you A - A - A)?


In the first case, yes, and in the second case, no.

On proving problems, often the two triangles in the figure look obviously congruent and so it may be hard to see what there is to prove. But you simply need to look for corresponding side and angle parts in the two triangles that are known to be the same length or same angle measure.

Two angles in a figure might be the same if they're vertical angles or corresponding angles, or base angles of a isosceles triangle. (Or it is given.)

Two sides might be the same length if they are halves of a longer line (there is a midpoint). Or, they ARE the same line. Or you have a rectangle or square somewhere. (Or, it is given.)

For example, the image below does NOT depict two congruent triangles.

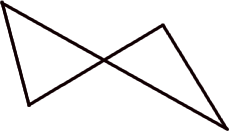
not congruent triangles

But this image does - because I made the point K to be a midpoint for the two intersecting line segments.

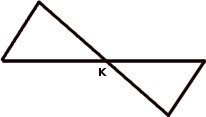
two congruent triangles

So there you have two pairs of lines of same length. And you have vertical angles which are the same - can you see how we then have S - A - S same in the two triangles -> they're congruent.

Maybe it would help to read explanations of this stuff a few times, from different places, with different wordings. It is not really difficult, I don't think!

Practice problems for congruent triangles from Yahoo education

Geometry: Congruent Triangles. Math for Morons like us.


Recognizing congruent triangles - interactive practice page from Oswego City School District Regents Exam Prep Center


Proving Rriangles Congruent interactive gizmo from ExploreLearning.com.
- you get 5 minutes free exploration time. It's a great site and great 'gizmos'.

What is proof - my own article.

Tags: , , , ,

Comments

Anonymous said…
I love your "I have a secret triangle" approach. I'll have to remember that to use with my students. We do a similar thing with "I have a secret number" as an introduction to algebra, but I hadn't thought to apply it to geometry. Excellent post, as usual!
11:41 AM, May 29, 2006
Anonymous said…
thanx
9:12 PM, January 09, 2008
Anonymous said…
not bad
7:57 AM, July 18, 2010
Post a Comment

Popular posts from this blog

Conversion chart for measuring units

Image
I was just sent a link to this site; all it is, is a handy one-page printable conversion chart for various US measures, metric measures, and US vs. metric measures. Includes even a comparative Fahrenheit vs. Celsius thermometer. http://metricconversioncharts.org/
Read more

Geometric art project: seven-circle flower design

Image
I got inspired by the blogpost Art School | Geometric Design with Islamic Art where Deborah shows how to make a neat flower design with seven circles , using a compass, and then coloring it using 2, 3, or 4 colors (or however many of your own). I think it ties in neatly with mathematics, and lets students practice drawing circles with a compass.  My girls loved the art/math project. Here are pictures they made: Here are step-by-step instructions for the flower design: 1.  Draw a line and a circle so that the circle's center point is on the line. Then mark the points where this circle intersects the line. 2. Use those points as center points, and draw two more circles. The radius is the same all the time, so make sure you don't change it on your compass!We used 5 cm as the radius, and that made the whole design fit neatly on a regular letter size paper. 3. Now note the two points marked in the picture. They will be used as center points in the next
Read more

Meaning of factors in multiplication: four groups of 2, or 4 taken two times?

Someone asked me about the interpretation or meaning of the two numbers in multiplication, such as 4 × 2. Do you view it as four groups of 2 , or as four, taken two times ? Here's their question: "...I noticed that your explanation about how to interpret a math phrase, such as 4 × 2, is different from how I have understood it and taught it to my older daughter who was using RightStart Math at this level. Let me explain:  I see that you are using the first factor to denote number of groups and the second factor tells how many are in each group (4 × 2 would be interpreted 4 groups of 2).  On the other hand, I have taught and thought of it reversed, with the first factor telling how many are in each group and the second factor telling you how many groups (4 × 2 would be 4 taken 2 times).  I know that the difference in explanations does not ultimately change the product, but I am wondering what you thoughts are.  When I conceptually picture what I'm doing I see it as 4
Read more