What is calculus?
I recently read a calculus book (actually two) that brought me to reflect what IS calculus.
First of all, let me state what calculus is not:
So what is calculus? It is basically the mathematics of change. Calculus allows us to study a thing that's changing (represented by some function), and the RATE of that change.
I'll give you an example.
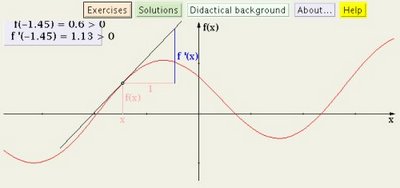
Suppose you have a graph like the one below. Maybe this function (the red one) is depicting how temperature (or voltage or some other thing) changes over time.
The black straight line is a tangent to the function - in other words it "touches" the function in one point. The steepness of the tangent tells us how steep the function itself is going at that point.
Imagine that the tangent (the black straight line) was drawn into a point a little further on the red graph. The red function is increasing but it's coming to a 'hill'. When nearing the hilltop, the tangent wouldn't be as steep as the one that is drawn. It would be less "slanted".
The steepness of the tangent tells us HOW quickly the function itself is changing at that point. And that is one fundamental idea of calculus - the derivative - rate of change. Not just change but rate of change, how quickly the change is taking place.
You can see this picture plus some derivative puzzles at Maths Online Gallery.
Calculus is called the pillar or foundation of modern mathematics. It is the form of math that has allowed us to have our modern technology. Calculus is used extensively in all engineering, physics, biology, chemistry, economy, and other sciences. It allows people to study change, rate of change, and points where the rate of change is zero - maxima and minima.
I liked calculus a lot in my university studies. It seemed to me to be powerful, awesome stuff. And I'm not alone in feeling that way:
Tags: math
First of all, let me state what calculus is not:
- Calculus is NOT the epitome of math, the highest mathematics there is, or anything such like.
So what is calculus? It is basically the mathematics of change. Calculus allows us to study a thing that's changing (represented by some function), and the RATE of that change.
I'll give you an example.

Suppose you have a graph like the one below. Maybe this function (the red one) is depicting how temperature (or voltage or some other thing) changes over time.
The black straight line is a tangent to the function - in other words it "touches" the function in one point. The steepness of the tangent tells us how steep the function itself is going at that point.
Imagine that the tangent (the black straight line) was drawn into a point a little further on the red graph. The red function is increasing but it's coming to a 'hill'. When nearing the hilltop, the tangent wouldn't be as steep as the one that is drawn. It would be less "slanted".
The steepness of the tangent tells us HOW quickly the function itself is changing at that point. And that is one fundamental idea of calculus - the derivative - rate of change. Not just change but rate of change, how quickly the change is taking place.
You can see this picture plus some derivative puzzles at Maths Online Gallery.
Calculus is called the pillar or foundation of modern mathematics. It is the form of math that has allowed us to have our modern technology. Calculus is used extensively in all engineering, physics, biology, chemistry, economy, and other sciences. It allows people to study change, rate of change, and points where the rate of change is zero - maxima and minima.
I liked calculus a lot in my university studies. It seemed to me to be powerful, awesome stuff. And I'm not alone in feeling that way:
"...think of it as a hike over a mountain pass. Yes it's hard work to trudge up the slopes. And yes, you long to rest in the valley that lies on the other side. But the view from up there is breathtaking."
Karl Hahn
"...every once in a while, one of these concepts smacks us on the head, and, after we recover from the stun, we all "Ohhhhh!" together in understanding and awe of the power of mathematics."
Fairfield High School
AP Calcucus Home Page
Tags: math

Comments
Sounds like a bunch of physicists and engineers talking to me. Most mathematicians, on the other hand, take it as an article of faith that Zermelo-Frankle set theory is the foundation of modern mathematics. However, logicians know the disturbing reality that there are no foundations!