Teaching long multiplication a.k.a multiplying in columns)
The two videos below show how you could teach multi-digit multiplication, or the multiplication algorithm, or multiplying in columns to students.
I approach this in steps. First, to teach students to multiply 4 × 87 or 5 × 928 (one factor is single-digit):
1) Teach students to multiply single-digit numbers by whole tens and hundreds.
2) Teach them the partial products algorithm;
3) Use the above as a stepping stone and teach the usual multiplication algorithm.
Then we can go on to the two-digit multiplier:
4) Teach the partial products again.
5) Teach the regular form of the algorithm.
Let's look at these steps in more detail.
Step 1. This means teaching students to multiply 5 × 80 or 7 × 400 or 3 × 40 or 9 × 900 (mentally!). The shortcut is to multiply without the zero or zeros, then tag the zero or zeros to the result.
But, where does it come from? For example, 5 × 80 is the same as 5 × 8 × 10. We first multiply 5 × 8 and then multiply that result by 10.
Step 2 is the partial products algorithm. Here, we write the numbers under each other, just like in the regular multiplication algorithm. But the multiplying is done in two (or three) parts: first the ones, then the tens, and then the hundreds (if any).
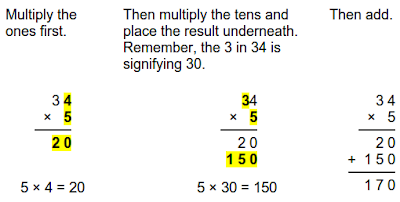
Step 3. After this, you would teach the usual multiplication algorithm. Point out to students how the two multiplications and the addition (the carry) are done at the same time, instead of as separate calculations.
This step needs practiced quite a bit before moving on so that students become confident in the carrying process.
Step 4a has to do with learning to multiply 50 × 46 or 70 × 352 or 600 × 529 in columns, using the regular algorithm. It is like multiplying 5 × 46 and tagging a zero, or multiplying 6 × 529 and tagging two zeros, but we place those extra zeros in the result first, before multiplying.
The bolded and underlined zeros are placed there before multiplying. The second video makes this maybe even clearer.
Step 4b has to do with multiplications by a 2-digit multiplier, such as 45 × 89. Here, we'd first multiply 40 × 89, then 5 × 89 (using the regular algorithm), and then add the two results. So this means, first of all, three separate calculations.
Step 5: We show students the regular form of the multiplying in columns with a two-digit multiplier, and point out how those three separate calculations are now compactly written under each other.
That's it in a nutshell! Please watch the videos to make this even more clear.
Teaching multiplication algorithm
Multiplication algorithm with a 2-digit multiplier
I approach this in steps. First, to teach students to multiply 4 × 87 or 5 × 928 (one factor is single-digit):
1) Teach students to multiply single-digit numbers by whole tens and hundreds.
2) Teach them the partial products algorithm;
3) Use the above as a stepping stone and teach the usual multiplication algorithm.
Then we can go on to the two-digit multiplier:
4) Teach the partial products again.
5) Teach the regular form of the algorithm.
Let's look at these steps in more detail.
Step 1. This means teaching students to multiply 5 × 80 or 7 × 400 or 3 × 40 or 9 × 900 (mentally!). The shortcut is to multiply without the zero or zeros, then tag the zero or zeros to the result.
But, where does it come from? For example, 5 × 80 is the same as 5 × 8 × 10. We first multiply 5 × 8 and then multiply that result by 10.
Step 2 is the partial products algorithm. Here, we write the numbers under each other, just like in the regular multiplication algorithm. But the multiplying is done in two (or three) parts: first the ones, then the tens, and then the hundreds (if any).
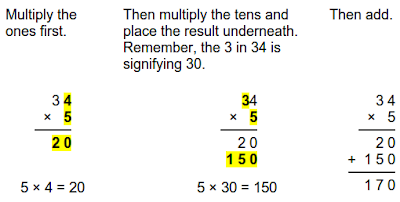
Step 3. After this, you would teach the usual multiplication algorithm. Point out to students how the two multiplications and the addition (the carry) are done at the same time, instead of as separate calculations.
This step needs practiced quite a bit before moving on so that students become confident in the carrying process.
Step 4a has to do with learning to multiply 50 × 46 or 70 × 352 or 600 × 529 in columns, using the regular algorithm. It is like multiplying 5 × 46 and tagging a zero, or multiplying 6 × 529 and tagging two zeros, but we place those extra zeros in the result first, before multiplying.
3 1 5
4 6 5 2 9
x 5 0 x 6 0 0
-------- ------------
2 3 0 0 3 1 7 4 0 0
The bolded and underlined zeros are placed there before multiplying. The second video makes this maybe even clearer.
Step 4b has to do with multiplications by a 2-digit multiplier, such as 45 × 89. Here, we'd first multiply 40 × 89, then 5 × 89 (using the regular algorithm), and then add the two results. So this means, first of all, three separate calculations.
Step 5: We show students the regular form of the multiplying in columns with a two-digit multiplier, and point out how those three separate calculations are now compactly written under each other.
That's it in a nutshell! Please watch the videos to make this even more clear.

Comments
http://www.videotutorials.co.nr/