The exponential function
I just finished reading the third volume of Calculus Without Tears... worksheets designed to teach calculus concepts before high school, for those interested.
So I've gotten a refresher on calculus... which I've always loved, and so that's why in today's post I hope to explain to you ONE little point from calculus - a fascinating and important one - that is.... THE EXPONENTIAL FUNCTION and THE NUMBER E.
First you need to know a calculus concept, and something about e:
Simple enough, huh?
Okay, so here we go:
There is a function....
whose growth rate at any point
is always
its value at that point!
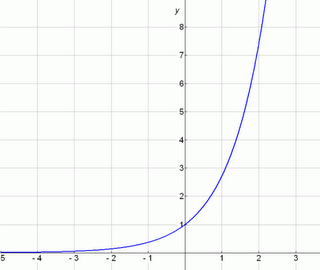
This is a remarkable property, and ex is the ONLY function with this property: that its growth rate at any point is the same as its value at that point.
But there is more:
You know how sine and cosine are 'waves' when their graphs are plotted. They don't look anything like the exponential function, which just shoots straight up!
BUT when you switch to the complex numbers, they all three are deeply connected with each other:
Isn't that something showing us the importance of the exponential function?
Then, who would have guessed that if you look at the sequence...
1 + 1/1
(1 + 1/2)2
(1 + 1/3)3
(1 + 1/4)4
(1 + 1/5)5
(1 + 1/6)6
(1 + 1/7)7
(1 + 1/8)8
(1 + 1/9)9.
.
.
.
...that it tends to e! (In other words, its limit is e as n → infinity.)
Check for yourself by using this nice interactive thing where you slide the sliding bar to change value of n.
This number e shows up everywhere!!! No wonder it is often compared to Pi, and those two together are like "GIANTS" or "biggies" when it comes to special numbers.
I hope your head is not spinning too fast (if you've never studied calculus before). I just wanted to show some 'glimpses' of the 'goodies' of calculus... it is fascinating. It's like anywhere mathematicians turn, they find Pi and e.... those two immensely important irrational numbers ... lots of connections in different areas of mathematics - and I don't know but a tiny fraction of those. All of it is beyond me... I stand in awe...
Tags: math, mathematics, calculus
So I've gotten a refresher on calculus... which I've always loved, and so that's why in today's post I hope to explain to you ONE little point from calculus - a fascinating and important one - that is.... THE EXPONENTIAL FUNCTION and THE NUMBER E.
First you need to know a calculus concept, and something about e:
- The steeper the graph of a function, the faster it's growing (and vice versa)
- We can measure the steepness of a function at any point by drawing a tangent, and checking the slope of the tangent.
- e is a VERY special irrational number with the approximate value 2.718281828459...
Simple enough, huh?
Okay, so here we go:
There is a function....
whose growth rate at any point
is always
its value at that point!

The function ex
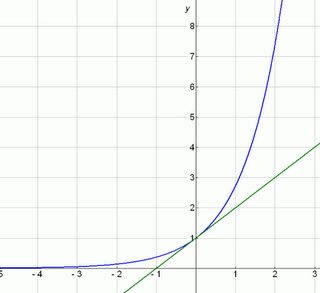
The 'steepness' of the tangent shows us the growth rate of the function.
Tangent drawn at x=0 has slope 1 - which is the value of ex when x=0.
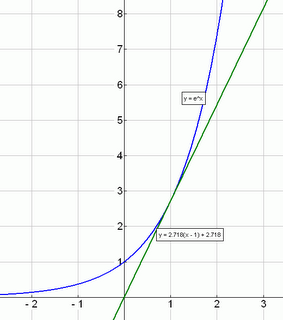
Here is a tangent to ex drawn at x=1.

Zooming in closer... The tangent drawn at x=1 has slope 2.718... - which is the value of ex at x=1.

The 'steepness' of the tangent shows us the growth rate of the function.
Tangent drawn at x=0 has slope 1 - which is the value of ex when x=0.

Here is a tangent to ex drawn at x=1.

Zooming in closer... The tangent drawn at x=1 has slope 2.718... - which is the value of ex at x=1.
This is a remarkable property, and ex is the ONLY function with this property: that its growth rate at any point is the same as its value at that point.
But there is more:
You know how sine and cosine are 'waves' when their graphs are plotted. They don't look anything like the exponential function, which just shoots straight up!
BUT when you switch to the complex numbers, they all three are deeply connected with each other:
eix = cos x + i sin x
(Euler's formula - e also gets its name from Euler)
ei&pi + 1 = 0
A special case of Euler's formula, linking five important numbers e, i, π, 1, and 0.
cos x = (eix + e-ix)/2
sin x = (eix - e-ix)/2i
These two expressions show that both cosine and sine can be written using exponential function alone.
(Euler's formula - e also gets its name from Euler)
ei&pi + 1 = 0
A special case of Euler's formula, linking five important numbers e, i, π, 1, and 0.
cos x = (eix + e-ix)/2
sin x = (eix - e-ix)/2i
These two expressions show that both cosine and sine can be written using exponential function alone.
Isn't that something showing us the importance of the exponential function?
Then, who would have guessed that if you look at the sequence...
1 + 1/1
(1 + 1/2)2
(1 + 1/3)3
(1 + 1/4)4
(1 + 1/5)5
(1 + 1/6)6
(1 + 1/7)7
(1 + 1/8)8
(1 + 1/9)9.
.
.
.
...that it tends to e! (In other words, its limit is e as n → infinity.)
Check for yourself by using this nice interactive thing where you slide the sliding bar to change value of n.
This number e shows up everywhere!!! No wonder it is often compared to Pi, and those two together are like "GIANTS" or "biggies" when it comes to special numbers.
With the possible exception of pi, e is the most important constant in mathematics since it appears in myriad mathematical contexts involving limits and derivatives.
(http://mathworld.wolfram.com/e.html)
As far as there being other nice numbers that come up all the time, e and Pi are certainly the two biggies. There's another number, called the golden ratio, which is (1+√5)/2. It doesn't look all that nice at first glance, but it has some nice properties too, and the Greeks liked it a lot. But it doesn't come up nearly as much as e or Pi, so I guess it's not on par with the giants.
Why is e so important - Ask Dr. Math®
I hope your head is not spinning too fast (if you've never studied calculus before). I just wanted to show some 'glimpses' of the 'goodies' of calculus... it is fascinating. It's like anywhere mathematicians turn, they find Pi and e.... those two immensely important irrational numbers ... lots of connections in different areas of mathematics - and I don't know but a tiny fraction of those. All of it is beyond me... I stand in awe...
Tags: math, mathematics, calculus

Comments