Constructing an equilateral triangle

Constructing an equilateral triangle using a compass and straightedge is really simple, as you probably know.

I feel it is a good project for students to explore and figure out how to do it. But here's how:

First you choose your side length. Here it is marked with the two dots.





Then you draw two circles, using the side length as the radius:




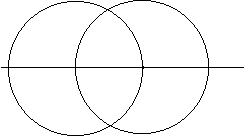
Where the circles intersect, is the third vertex of the triangle.



The beauty of this construction, I feel, is in how it exemplifies and applies the definitions of both circle and equilateral triangle.

You know, a circle is the set of those points that are at a given distance from the center point.

And an equilateral triangle is a triangle whose all sides have the same length.

This construction can help your student to truly grasp what these are. And it's simple enough.


After that, you would naturally introduce this problem:

Draw a triangle with given side lengths. For example, suppose you have these three 'sticks' or line segments given to you. Now draw a triangle.





The idea is exactly the same as before. But let them think about it and find it out. Can you figure it out?

Tags: ,

Comments

Anonymous said…
Thank you so much for teaching me how to do this! I was trying to make Christams decorations with old cards this past year and needed an equil. tri. I thought if I could figure it out it would be a great way to show my daughter the practical use of a triangle. This hits a home run...she read it with me this morning and said, "Mom, that makes so much sense. Let's do the card project this week." You're the Math Angel in our home.
9:39 AM, July 12, 2006
Post a Comment

Popular posts from this blog

Conversion chart for measuring units

Image
I was just sent a link to this site; all it is, is a handy one-page printable conversion chart for various US measures, metric measures, and US vs. metric measures. Includes even a comparative Fahrenheit vs. Celsius thermometer. http://metricconversioncharts.org/
Read more

Meaning of factors in multiplication: four groups of 2, or 4 taken two times?

Someone asked me about the interpretation or meaning of the two numbers in multiplication, such as 4 × 2. Do you view it as four groups of 2 , or as four, taken two times ? Here's their question: "...I noticed that your explanation about how to interpret a math phrase, such as 4 × 2, is different from how I have understood it and taught it to my older daughter who was using RightStart Math at this level. Let me explain:  I see that you are using the first factor to denote number of groups and the second factor tells how many are in each group (4 × 2 would be interpreted 4 groups of 2).  On the other hand, I have taught and thought of it reversed, with the first factor telling how many are in each group and the second factor telling you how many groups (4 × 2 would be 4 taken 2 times).  I know that the difference in explanations does not ultimately change the product, but I am wondering what you thoughts are.  When I conceptually picture what I'm doing I see i...
Read more

Geometric art project: seven-circle flower design

Image
I got inspired by the blogpost Art School | Geometric Design with Islamic Art where Deborah shows how to make a neat flower design with seven circles , using a compass, and then coloring it using 2, 3, or 4 colors (or however many of your own). I think it ties in neatly with mathematics, and lets students practice drawing circles with a compass.  My girls loved the art/math project. Here are pictures they made: Here are step-by-step instructions for the flower design: 1.  Draw a line and a circle so that the circle's center point is on the line. Then mark the points where this circle intersects the line. 2. Use those points as center points, and draw two more circles. The radius is the same all the time, so make sure you don't change it on your compass!We used 5 cm as the radius, and that made the whole design fit neatly on a regular letter size paper. 3. Now note the two points marked in the picture. They will be used as center points in the next...
Read more