Measuring sine
I get lots of questions, seemingly, about sine. It's because one of my pages with that topic ranks well in search engines and has the comment box in the end. Here's another one:
Well, you don't measure the sine per se. You measure certain sides of the triangle, and then calculate the sine.
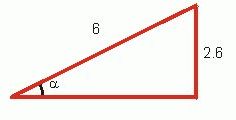
For example, in this picture, if we want to find the sine of the angle α, we measure the opposite side and the hypotenuse. They are already given as 2.6 and 6 units. Then just take their ratio: 2.6/6 and that's your sin α.
You might also enjoy reading my lesson about sine in a right triangle.
Tags: math, trigonometry
how to measure right triangle sine?
Well, you don't measure the sine per se. You measure certain sides of the triangle, and then calculate the sine.

For example, in this picture, if we want to find the sine of the angle α, we measure the opposite side and the hypotenuse. They are already given as 2.6 and 6 units. Then just take their ratio: 2.6/6 and that's your sin α.
You might also enjoy reading my lesson about sine in a right triangle.
Tags: math, trigonometry

Comments
sin(x) = x - x^3/3! + x^5/5! - x^7/7! + ...
+ (-1^n)(x^(2n+1))/(2n+1)! ...
where x is in radians. Oh, you started with an angle in degrees? Convert to radians this way:
r = d * pi / 180
where pi = 3.14159265...
What is 3! (?). That's 3 factorial. That's 3 * 2 * 1 = 6. 5! is 5 * 4 * 3 * 2 * 1 = 120. A short cut is that 5! = 3! * 4 * 5. You already figured out 3!.
This formula converges pretty quickly. When you do the next iteration and the answer hasn't changed in a way that you care about, stop.